Special cases of the sum and difference formulas for sine and cosine yields what is known as the double-angle identities and the half-angle identities. First, using the sum identity for the sine,
sin 2α = sin (α + α)
sin 2α = sin α cos α + cos α sin α
sin 2α = 2 sin α cos α
Similarly for the cosine,
Using the Pythagorean identity, sin2 α+cos2α=1, two additional cosine identities can be derived.
and
The half-angle identities for the sine and cosine are derived from two of the cosine identities described earlier.
The sign of the two preceding functions depends on the quadrant in which the resulting angle is located.
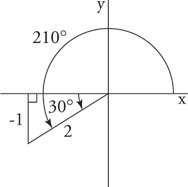
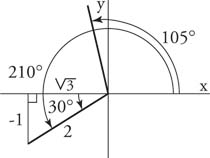
Example 1: Find the exact value for sin 105° using the half-angle identity.
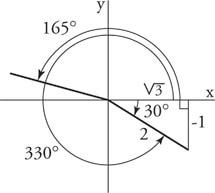
In the following verification, remember that 105° is in the second quadrant, and sine functions in the second quadrant are positive. Also, 210° is in the third quadrant, and cosine functions in the third quadrant are negative. From Figure 1 , the reference triangle of 210° in the third quadrant is a 30°–60°–90° triangle. Therefore, cos 210° = −cos 30°.
|
|
|
| Figure 1 | Drawing for Example 1. |
|
|
|
|
|
| Figure 2 | Drawing for Example 2. |
|
|
Example 3: Use the double-angle identity to find the exact value for cos 2
x given that sin
x =
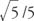
.
Because sin x is positive, angle x must be in the first or second quadrant. The sign of cos 2 xwill depend on the size of angle x. If 0° < x < 45° or 135° < x < 180°, then 2 x will be in the first or fourth quadrant and cos2 x will be positive. On the other hand, if 45° < x < 90° or 90° <x < 135”, then 2 x will be in the second or third quadrant and cos 2 x will be negative.
Example 4: Verify the identity 1 − cos 2 x = tan x sin 2 x.
|
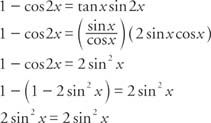
Tangent IdentitiesFormulas for the tangent function can be derived from similar formulas involving the sine and cosine. The sum identity for tangent is derived as follows:
To determine the difference identity for tangent, use the fact that tan(−β) = −tanβ.
Example 1: Find the exact value of tan 75°. Because 75° = 45° + 30°
Example 2: Verify that tan (180° − x) = −tan x.
Example 3: Verify that tan (180° + x) = tan x.
Example 4: Verify that tan (360° − x) = − tan x.
The preceding three examples verify three formulas known as the reduction identities for tangent. These reduction formulas are useful in rewriting tangents of angles that are larger than 90° as functions of acute angles. The double-angle identity for tangent is obtained by using the sum identity for tangent.
The half-angle identity for tangent can be written in three different forms.
In the first form, the sign is determined by the quadrant in which the angle α/2 is located. Example 5: Verify the identity
Example 6: Verify the identity tan (α/2) = (1 − cos α)/sin α.
Example 7: Verify the identity tan (α − 2) = sin π/(1 + cos α). Begin with the identity in Example 6.
Example 8: Use a half-angle identity for the tangent to find the exact value for tan 15°. What follows are two alternative solutions.
|
|
The process of converting sums into products or products into sums can make a difference between an easy solution to a problem and no solution at all. Two sets of identities can be derived from the sum and difference identities that help in this conversion. The following set of identities is known as the product-sum identities.
These identities are valid for degree or radian measure whenever both sides of the identity are defined.
Example 1: Verify that sin α cos β =
Start by adding the sum and difference identities for the sine.
The other three product-sum identities can be verified by adding or subtracting other sum and difference identities.
Example 2: Write cos 3 x cos 2 x as a sum.
Alternate forms of the product-sum identities are the sum-product identities.
These identities are valid for degree or radian measure whenever both sides of the identity are defined.
Example 3:
Solve for α by adding the following two equations and then dividing by 2. Solve for β by subtracting the two equations and then dividing by 2.
Example 4: Write the difference cos 8α − cos 2 α as a product.
Example 5: Find the exact value of sin 75° + sin 15°.
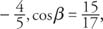 and α and β are fourth quadrant angles.
and α and β are fourth quadrant angles.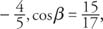 and α and β are fourth quadrant angles.
and α and β are fourth quadrant angles.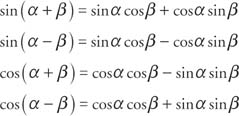
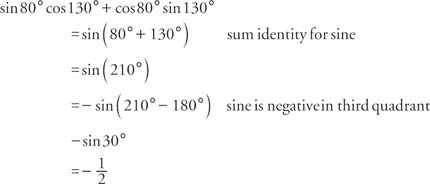
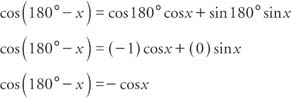
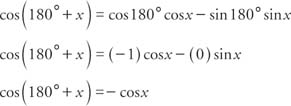
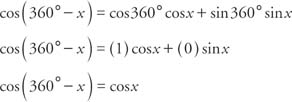
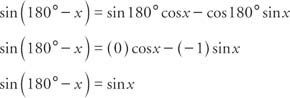
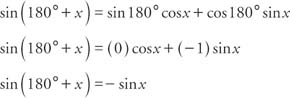
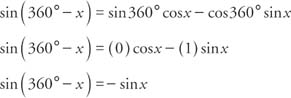
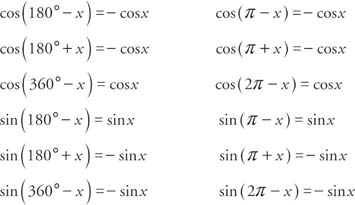
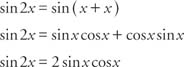
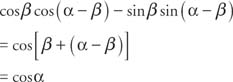
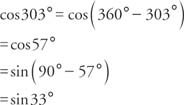
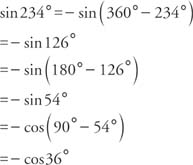
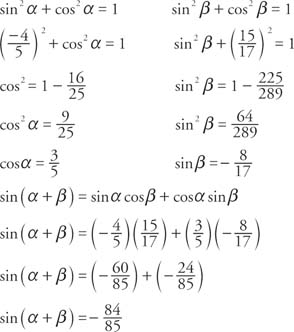
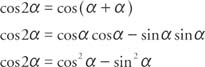
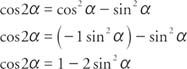
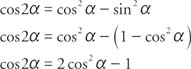
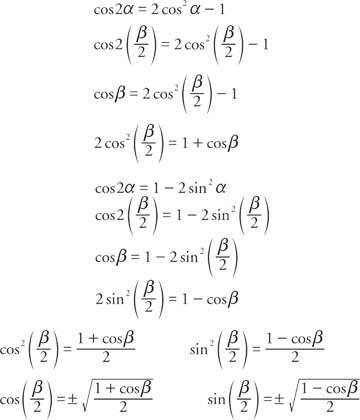
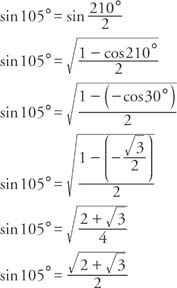
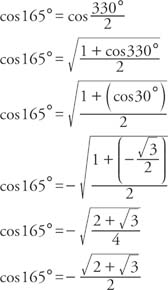
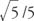 .
.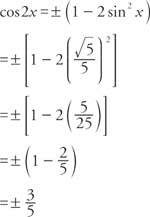
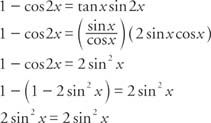
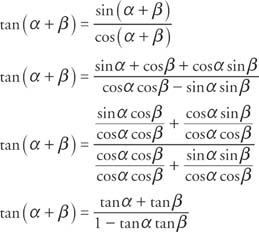
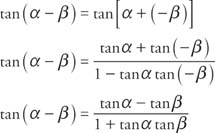
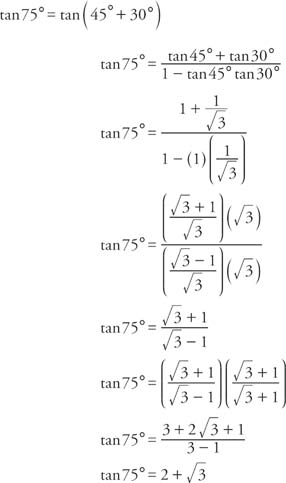
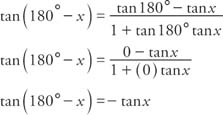
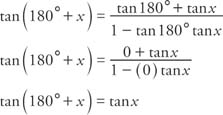
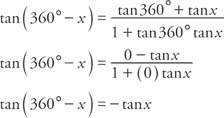
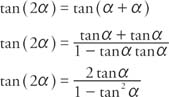
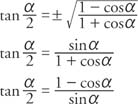


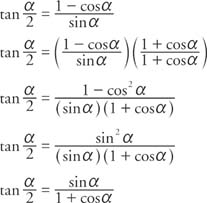

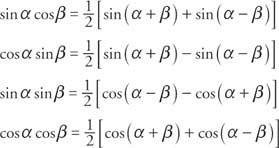
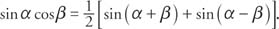
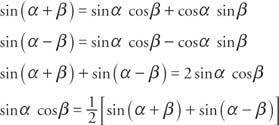
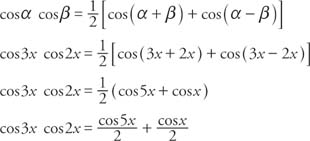
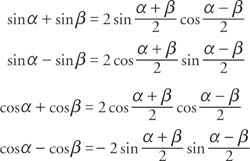
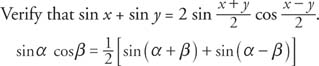
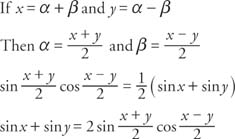
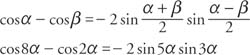
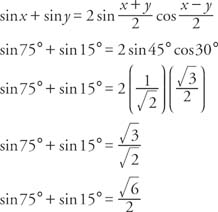
Hiç yorum yok:
Yorum Gönder